14+ Basic Integration Formulas List
Basic Integration Formulas List. Integration by parts the standard formulas for integration by parts are, bb b aa a ∫∫ ∫ ∫udv uv vdu=−= udv uv vdu− choose uand then compute and dv du by differentiating u and compute v by using the fact that v dv=∫. When choosing uand dv, we want a uthat will become simpler (or at least no more complicated) when we
 Pin by Tony Wong on karim Studying math, Mathematics From pinterest.com
Pin by Tony Wong on karim Studying math, Mathematics From pinterest.com
X dx x 1 8. ( ) 3 x dx x 3 5 6. The following table lists integration formulas side by side with the corresponding differentiation formulas.
Pin by Tony Wong on karim Studying math, Mathematics
- ∫ 1 d x = x + c. A s2 1 area of a triangle: ∫x n = x n+1 /n+1 + c. Z udv= uv z vdu integration by parts (which i may abbreviate as ibp or ibp) \undoes the product rule.
 Source: in.pinterest.com
Source: in.pinterest.com
Using the fundamental theorems of integrals, there are generalized. ∫sec x tan x = sec x + c. ( ) 3 x dx x 3 5 6. Of all the techniques we’ll be looking at in this class this is the technique that students are most likely to run into down the road in other classes. ∫cos x = sin.
 Source: mpec.sc.mahidol.ac.th
Source: mpec.sc.mahidol.ac.th
(12 9 )x x dx4 3 2 2 4 7. Integration formulas z dx = x+c (1) z xn dx = xn+1 n+1 +c (2) z dx x = ln|x|+c (3) z ex dx = ex +c (4) z ax dx = 1 lna ax +c (5) z lnxdx = xlnx−x+c (6) z sinxdx = −cosx+c (7) z cosxdx =.
 Source: teachoo.com
Source: teachoo.com
Dx x xx 1 5. (12 9 )x x dx4 3 2 2 4 7. In other words, integration is the process of continuous addition and the variable “c” represents the constant of integration. Integrating both sides and solving for one of the integrals leads to our integration by parts formula: Basic integration formulas and the substitution rule 1the second.
 Source: pinterest.com
Source: pinterest.com
- ∫ [ f ( x)] n f ′ ( x) d x = [ f ( x)] n + 1 n + 1. Dx x xx 1 5. Basic integration formulas and the substitution rule 1the second fundamental theorem of integral calculus recall fromthe last lecture the second fundamental theorem ofintegral calculus. ∫ eax + b = 1 aeax.
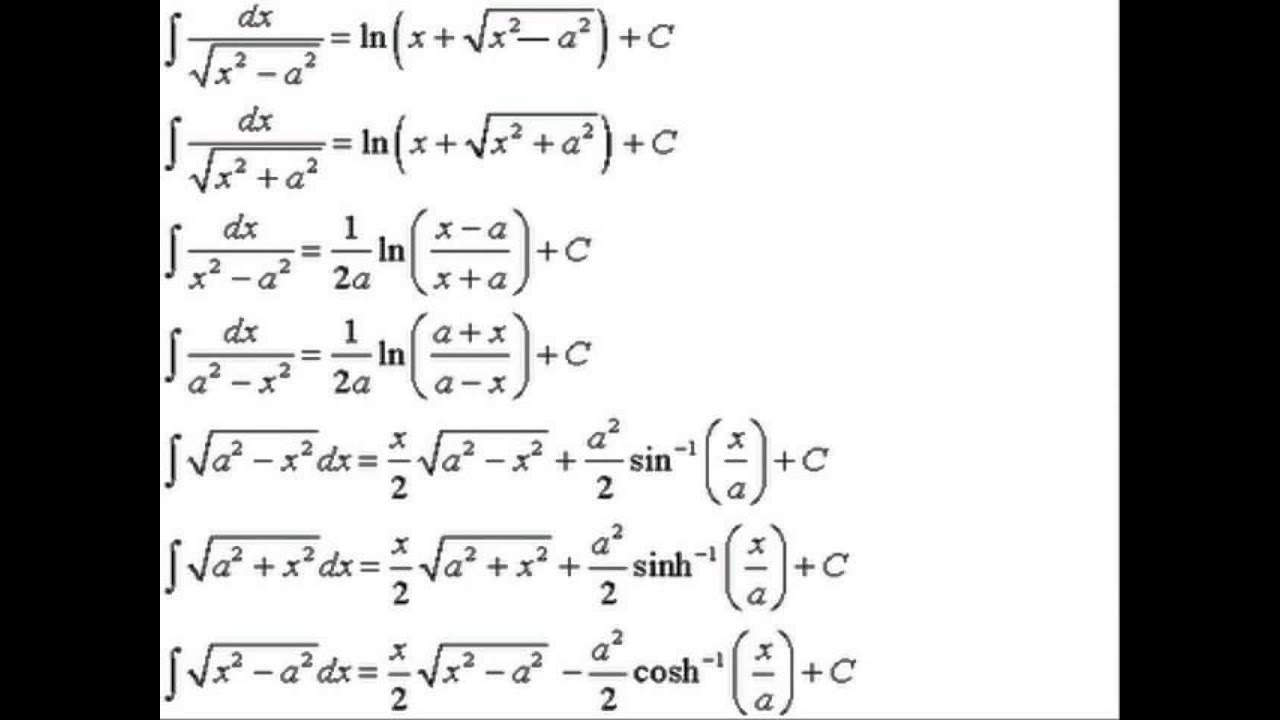 Source: youtube.com
Source: youtube.com
- ∫ a d x = a x + c where a is any constant. Integrating both sides and solving for one of the integrals leads to our integration by parts formula: N 6= 1 (2) z 1 x dx = lnjxj (3) z u dv = uv z vdu (4) z e xdx = e (5) z ax dx.
 Source: trigonometri-logaritma.blogspot.com
Source: trigonometri-logaritma.blogspot.com
- ∫ 1 d x = x + c. We write the integrals as the sum of two integrals and calculate them separately: 4sin 3 x dx 19. ∫x n = x n+1 /n+1 + c. Each formula for the derivative of a specific function corresponds to a formula for the derivative of an elementary function.